Prefix and Infix Operators for Persistence Landscapes
Rcpp_PersistenceLandscape-methods.RdPerform arithmetic on persistence landscapes.
# S4 method for class 'Rcpp_PersistenceLandscape,missing'
e1 + e2
# S4 method for class 'Rcpp_PersistenceLandscape,Rcpp_PersistenceLandscape'
e1 + e2
# S4 method for class 'Rcpp_PersistenceLandscape,missing'
e1 - e2
# S4 method for class 'Rcpp_PersistenceLandscape,Rcpp_PersistenceLandscape'
e1 - e2
# S4 method for class 'numeric,Rcpp_PersistenceLandscape'
e1 * e2
# S4 method for class 'Rcpp_PersistenceLandscape,numeric'
e1 * e2
# S4 method for class 'Rcpp_PersistenceLandscape,numeric'
e1/e2
# S4 method for class 'Rcpp_PersistenceLandscape,Rcpp_PersistenceLandscape'
x %*% yValue
A persistence landscape (an object of S4 class 'Rcpp_PersistenceLandscape').
Details
Most of these operators extend selected members of the S4 Arith group generic to the 'Rcpp_PersistenceLandscape' class:
unary and binary + and - for persistence landscapes, *, and / for
one persistence landscape (either factor or the numerator) and one numeric
(either factor or the denominator). The exception is the binary %*%,
which extends matrix multiplication to the inner product
on persistence landscapes.
See also
base::Arithmetic and base::matmult for base methods; arithmetic for function syntax and extensions.
Examples
# infix arithmetic with two landscapes
pt1 <- tdaunif::sample_torus_tube(100, 2.5)
pt2 <- tdaunif::sample_torus_tube(100, 2.5)
pd1 <- ripserr::vietoris_rips(pt1, dim = 2L, threshold = 3)
#> Warning: `dim` parameter has been deprecated; use `max_dim` instead.
pd2 <- ripserr::vietoris_rips(pt2, dim = 2L, threshold = 3)
#> Warning: `dim` parameter has been deprecated; use `max_dim` instead.
pl1 <- pl_new(pd1, degree = 1L, exact = TRUE)
pl2 <- pl_new(pd2, degree = 1L, exact = TRUE)
# plot
par(mfrow = c(3L, 2L), mar = c(0, 2, 0, 2))
# position? positing? (sticking a plus sign in front leaves something unchanged)
plot(+pl1)
plot(+pl2)
# negation
plot(-pl1)
# scalar multiplication
plot(pl2 * 3)
# addition & other-way scalar multiplication
plot(pl1 + 2 * pl2)
# subtraction and scalar division
plot(pl1 - pl2 / 2)
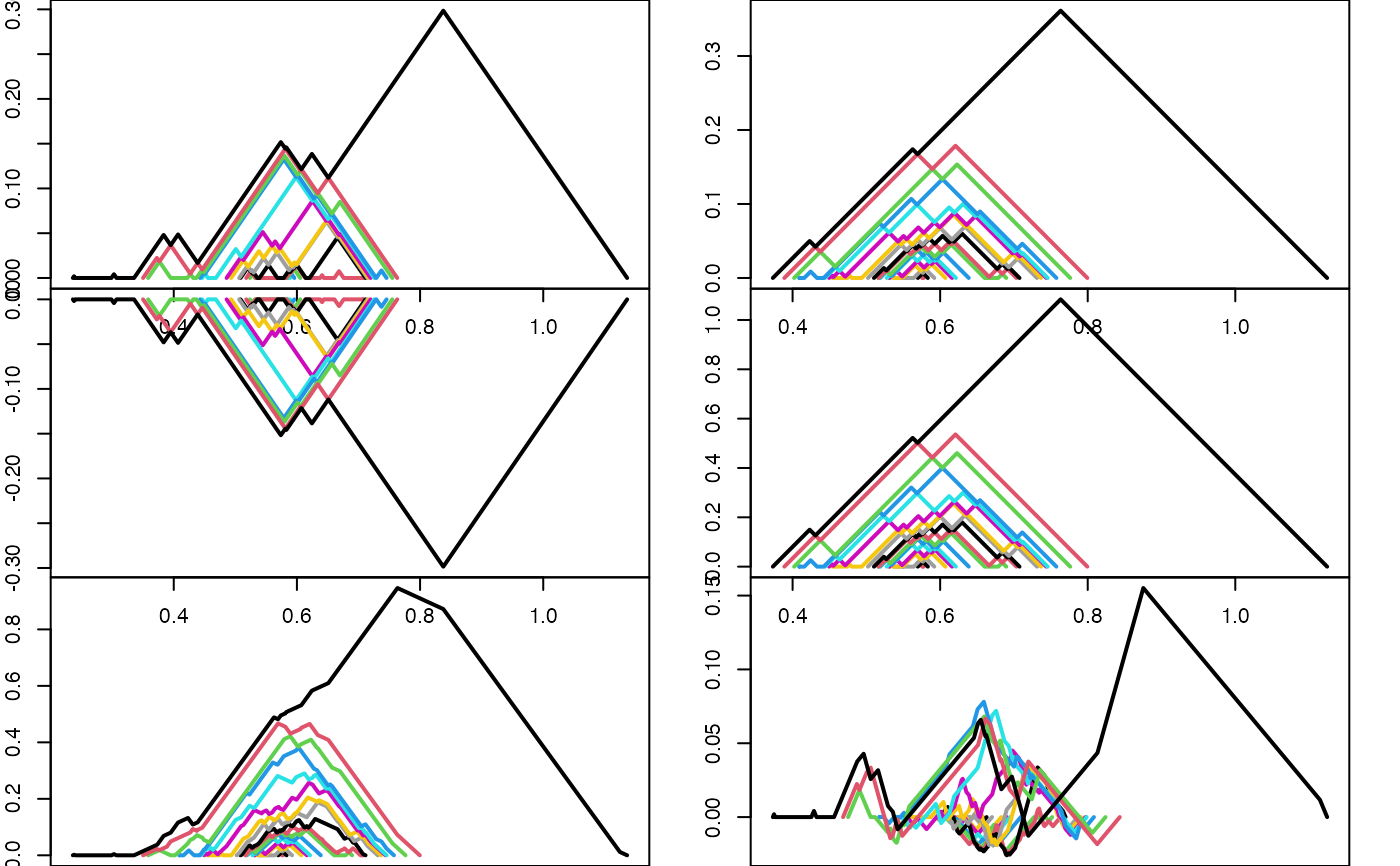 par(mfrow = c(1, 1), mar = c(5.1, 4.1, 4.1, 2.1))
# add an exact landscape to a discrete one
pl2d <- pl_new(pd2, degree = 1, exact = FALSE,
xmin = 0, xmax = 1.2, xby = 0.001)
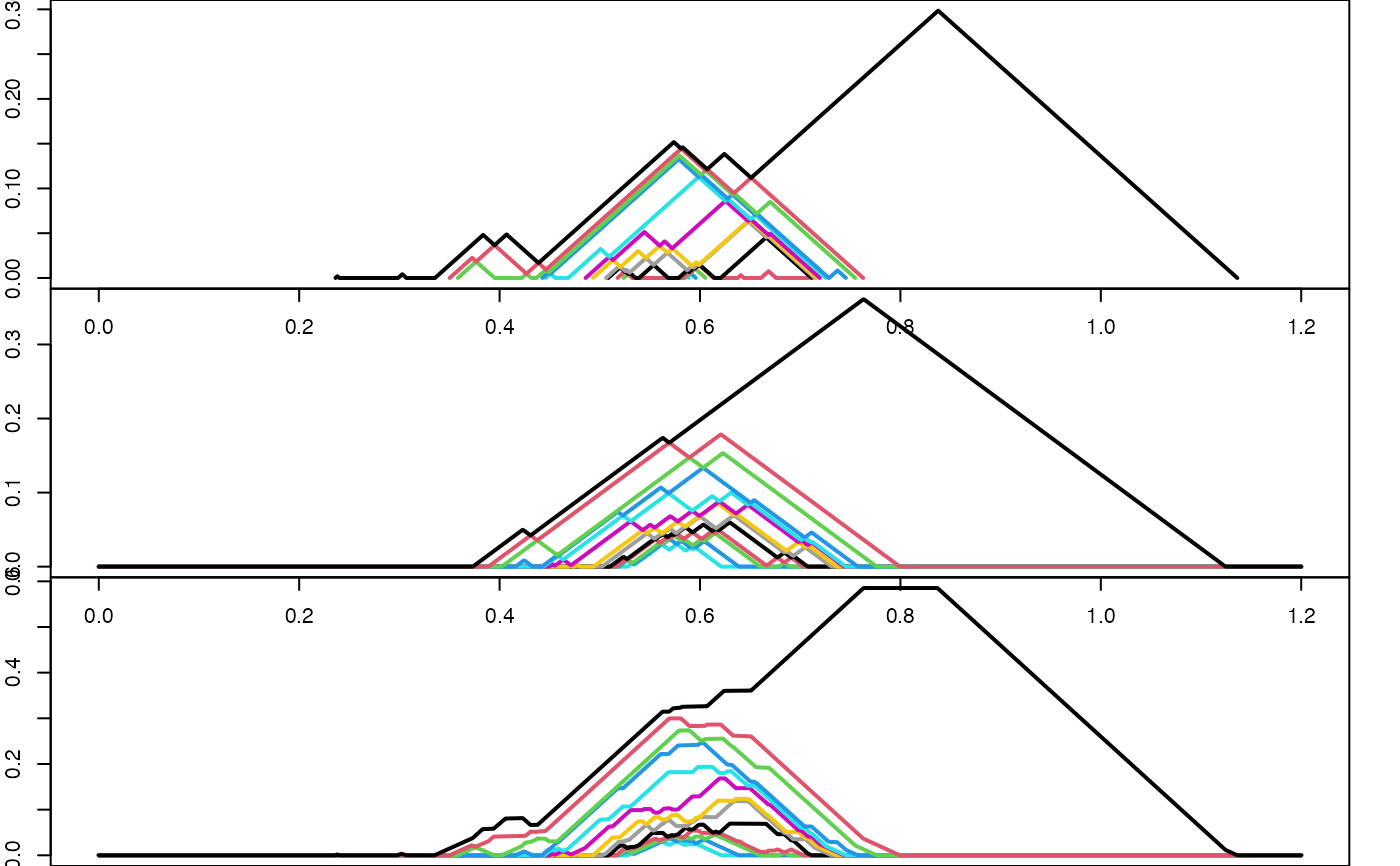
# plot the summand landscapes and their sum with consistent parameters;
# the exact landscape is automatically converted to a discrete one
n_lev <- pl_num_levels(pl1)
par(mfrow = c(3, 1), mar = c(0, 2, 0, 2))
plot(pl1, xlim = c(0, 1.2), n_levels = n_lev)
plot(pl2d, xlim = c(0, 1.2), n_levels = n_lev)
plot(pl1 + pl2d, xlim = c(0, 1.2), n_levels = n_lev)
par(mfrow = c(1, 1), mar = c(5.1, 4.1, 4.1, 2.1))
# add an exact landscape to a discrete one
pl2d <- pl_new(pd2, degree = 1, exact = FALSE,
xmin = 0, xmax = 1.2, xby = 0.001)
# plot the summand landscapes and their sum with consistent parameters;
# the exact landscape is automatically converted to a discrete one
n_lev <- pl_num_levels(pl1)
par(mfrow = c(3, 1), mar = c(0, 2, 0, 2))
plot(pl1, xlim = c(0, 1.2), n_levels = n_lev)
plot(pl2d, xlim = c(0, 1.2), n_levels = n_lev)
plot(pl1 + pl2d, xlim = c(0, 1.2), n_levels = n_lev)
 par(mfrow = c(1, 1), mar = c(5.1, 4.1, 4.1, 2.1))
# inner products of equal or similar landscapes
pl2 %*% pl2
#> [1] 0.04529366
pl2d %*% pl2d
#> [1] 0.04529371
pl2 %*% pl2d
#> [1] 0.04526804
if (FALSE) { # \dontrun{
set.seed(031537L)
# compute exact landscape for a large sample
pt <- tdaunif::sample_torus_tube(600, 2.5)
pd <- ripserr::vietoris_rips(pt, dim = 2, threshold = 3)
pl <- pl_new(pd, degree = 1, exact = TRUE)
# compute exact landscapes for a large sample of small samples
pl_list <- c()
for (i in seq(100)) {
pti <- tdaunif::sample_torus_tube(100, 2.5)
pdi <- ripserr::vietoris_rips(pti, dim = 2, threshold = 3)
pli <- pl_new(pdi, degree = 1L, exact = TRUE)
pl_list <- c(pl_list, pli)
}
# compute the mean exact landscape
pl_avg <- Reduce(`+`, pl_list) / length(pl_list)
# compute the distance between the exact landscapes
pl_diff <- pl - pl_avg
print(pl_diff %*% pl_diff)
} # }
par(mfrow = c(1, 1), mar = c(5.1, 4.1, 4.1, 2.1))
# inner products of equal or similar landscapes
pl2 %*% pl2
#> [1] 0.04529366
pl2d %*% pl2d
#> [1] 0.04529371
pl2 %*% pl2d
#> [1] 0.04526804
if (FALSE) { # \dontrun{
set.seed(031537L)
# compute exact landscape for a large sample
pt <- tdaunif::sample_torus_tube(600, 2.5)
pd <- ripserr::vietoris_rips(pt, dim = 2, threshold = 3)
pl <- pl_new(pd, degree = 1, exact = TRUE)
# compute exact landscapes for a large sample of small samples
pl_list <- c()
for (i in seq(100)) {
pti <- tdaunif::sample_torus_tube(100, 2.5)
pdi <- ripserr::vietoris_rips(pti, dim = 2, threshold = 3)
pli <- pl_new(pdi, degree = 1L, exact = TRUE)
pl_list <- c(pl_list, pli)
}
# compute the mean exact landscape
pl_avg <- Reduce(`+`, pl_list) / length(pl_list)
# compute the distance between the exact landscapes
pl_diff <- pl - pl_avg
print(pl_diff %*% pl_diff)
} # }