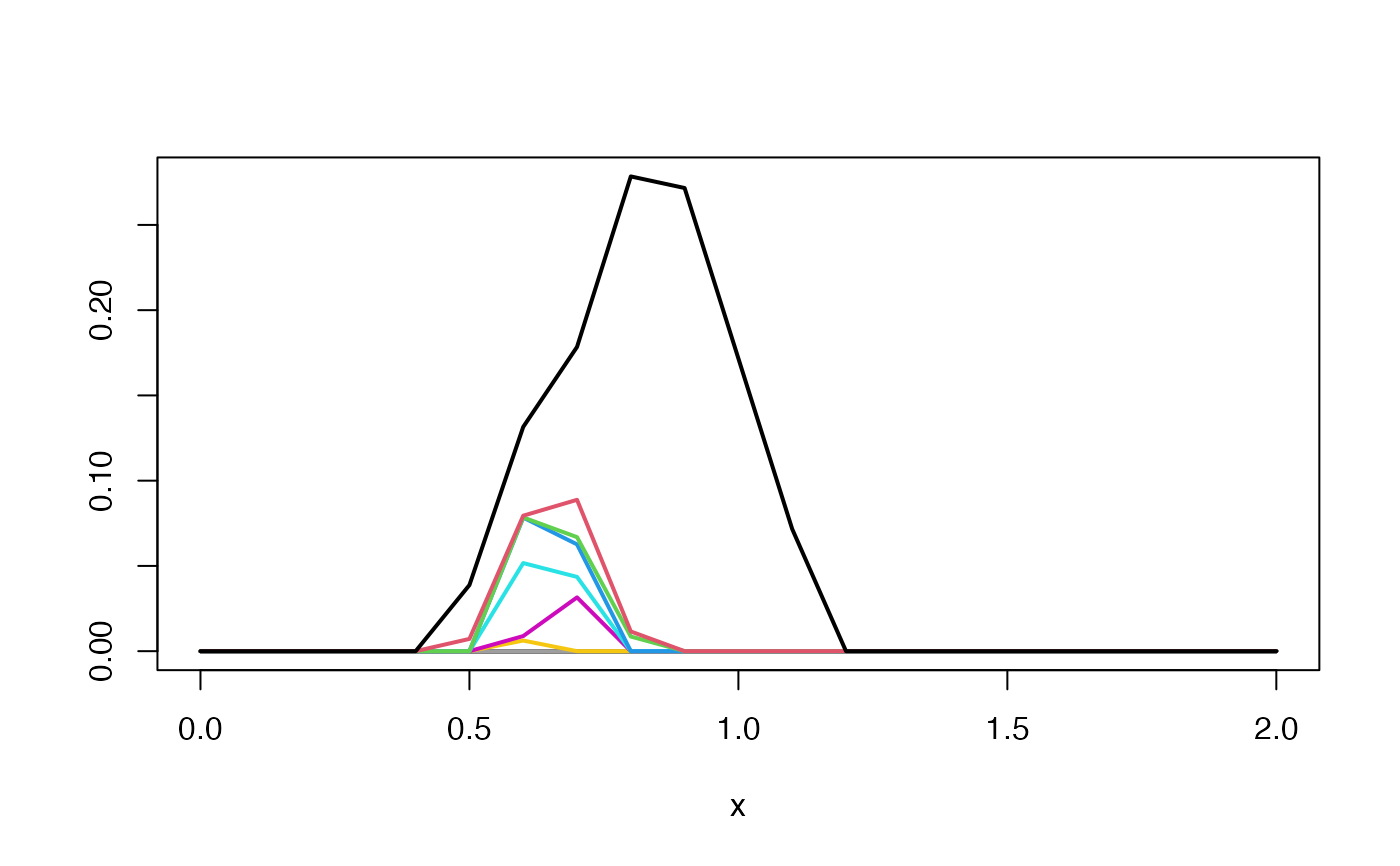Persistence Landscapes
landscape.RdCompute persistence landscapes from persistence data.
landscape(
pd,
degree = NULL,
exact = FALSE,
xmin = NULL,
xmax = NULL,
xby = NULL
)
pl_is_exact(pl)
pl_type(pl)
pl_num_levels(pl)
pl_limits(pl)
pl_support(pl)
pl_delimit(pl, xmin = NULL, xmax = NULL, xby = NULL)
pl_discretize(pl)Arguments
- pd
Persistence data (or diagram), stored as a 2-column matrix, as a 'persistence' object, or in a format coercible to 'persistence'.
- degree
Non-negative integer; if input is a persistence diagram object, then the dimension for which to compute a landscape. (For degree \(d\), the \((d+1)\)th matrix in the list will be selected.)
- exact
Set to
TRUEfor exact representation,FALSE(default) for discrete.- xmin, xmax
Domain thresholds for discrete PL; if not specified, then taken to be the support of the PL constructed from the data or the internal values of the 'Rcpp_PersistenceLandscape' object.
- xby
Domain grid diameter for discrete PL; if not specified, then set to the power of 10 that yields between 100 and 1000 intervals.
- pl
A persistence landscape as returned by
landscape().
Value
landscape() returns a persistence landscape (an object of S4 class
'Rcpp_PersistenceLandscape'). Other functions return summary information
about such an object.
Details
landscape() is a wrapper around the S4 class constructor
[methods:new()]. The pl_*() helper functions query a persistence
landscape as returned by landscape() for specific information or
manipulate its internal representation.
Use pl_is_exact() and pl_type() to get a landscape's internal
representation, pl_num_levels() its number of levels, pl_limits() the
endpoints of its internal representation (excluding infinities), and
pl_support() the infimum and supremum of its support (the points at which
its value is nonzero).
Use pl_delimit() to change the limits of a PL and pl_discretize() to
convert an exact landscape to a discrete one (using its internally-stored
range and resolution).
See also
Rcpp_PersistenceLandscape for the exported C++ class.
Examples
# sample points
points <- tdaunif::sample_torus_tube(100, 5)
# compute persistent homology
(pd <- ripserr::vietoris_rips(points, dim = 2L, threshold = 1))
#> Warning: `dim` parameter has been deprecated; use `max_dim` instead.
#> PHom object containing persistence data for 118 features.
#>
#> Contains:
#> * 99 0-dim features
#> * 17 1-dim features
#> * 2 2-dim features
#>
#> Radius/diameter: min = 0; max = 0.43814.
# compute persistence landscapes for 0-cycles
(pl <- landscape(pd, degree = 1, exact = TRUE))
#> Persistence landscape (exact format) of 8 levels over (0,0.438)
# first landscape layer
print(pl$getInternal()[[1L]])
#> [,1] [,2]
#> [1,] -Inf 0.000000000
#> [2,] 0.2147134 0.000000000
#> [3,] 0.2160738 0.001360426
#> [4,] 0.2174343 0.000000000
#> [5,] 0.2323197 0.000000000
#> [6,] 0.2407729 0.008453146
#> [7,] 0.2492260 0.000000000
#> [8,] 0.2780255 0.000000000
#> [9,] 0.2797984 0.001772880
#> [10,] 0.2815713 0.000000000
#> [11,] 0.2992309 0.000000000
#> [12,] 0.3306411 0.031410212
#> [13,] 0.3354987 0.026552628
#> [14,] 0.3487414 0.039795342
#> [15,] 0.3611506 0.027386169
#> [16,] 0.3859537 0.052189315
#> [17,] 0.4381430 0.000000000
#> [18,] Inf 0.000000000
# plot all landscape layers
plot(pl)
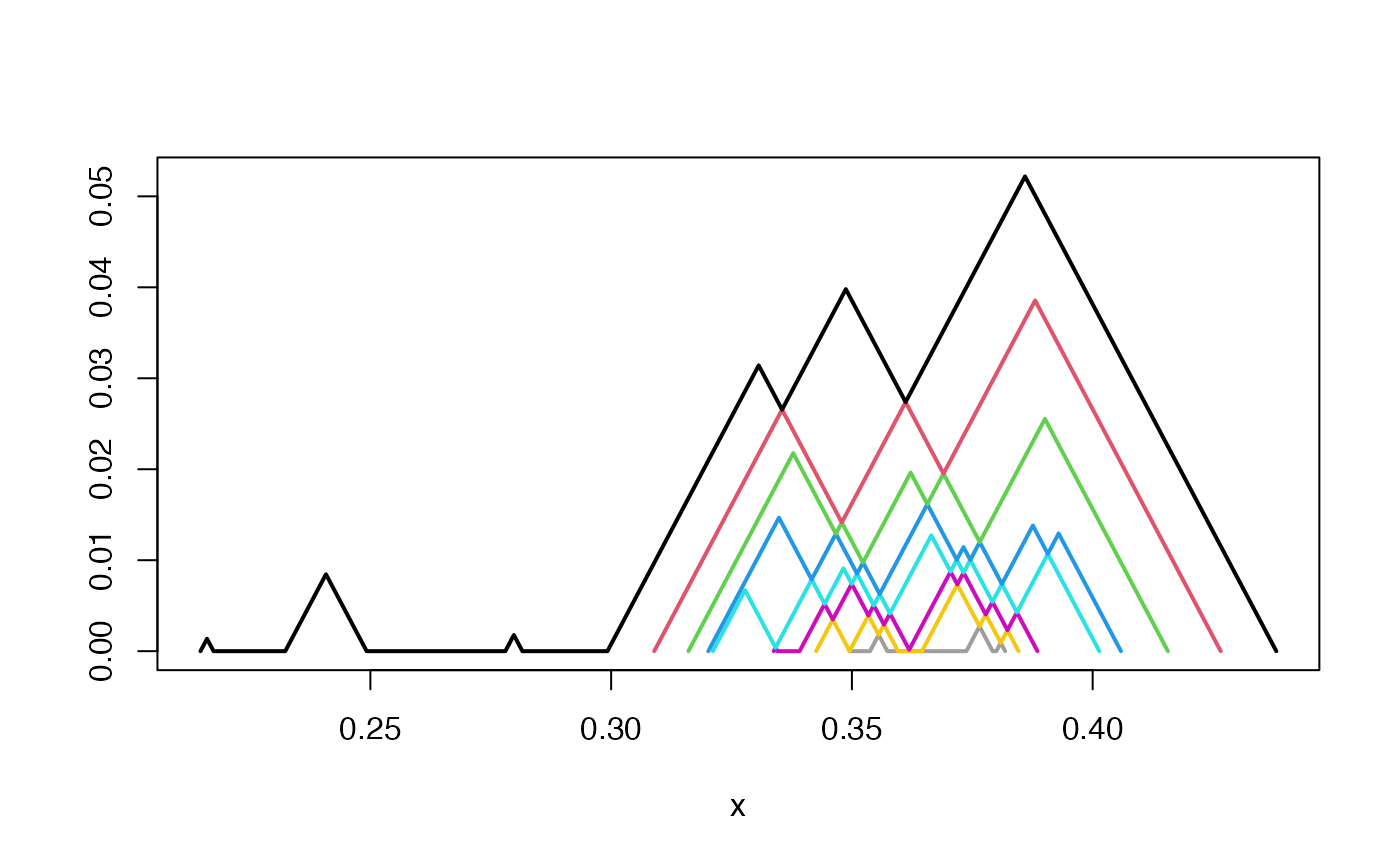 # coerce to discrete at different resolutions
plot(pl, xlim = c(0, .5))
# coerce to discrete at different resolutions
plot(pl, xlim = c(0, .5))
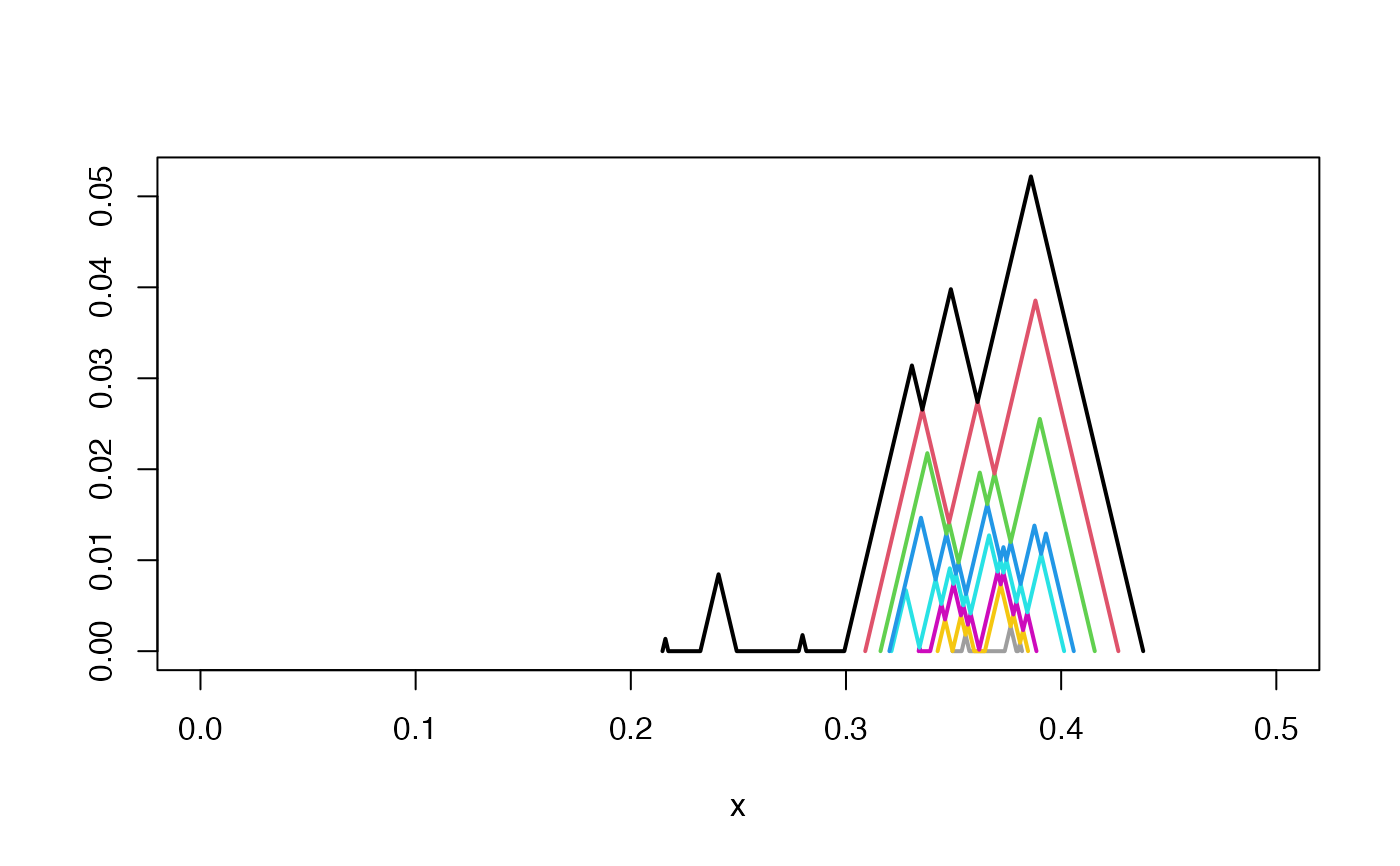 pl <- pl_delimit(pl, xmin = 0, xmax = .5, xby = .01)
pl_ <- pl_discretize(pl)
plot(pl_)
pl <- pl_delimit(pl, xmin = 0, xmax = .5, xby = .01)
pl_ <- pl_discretize(pl)
plot(pl_)
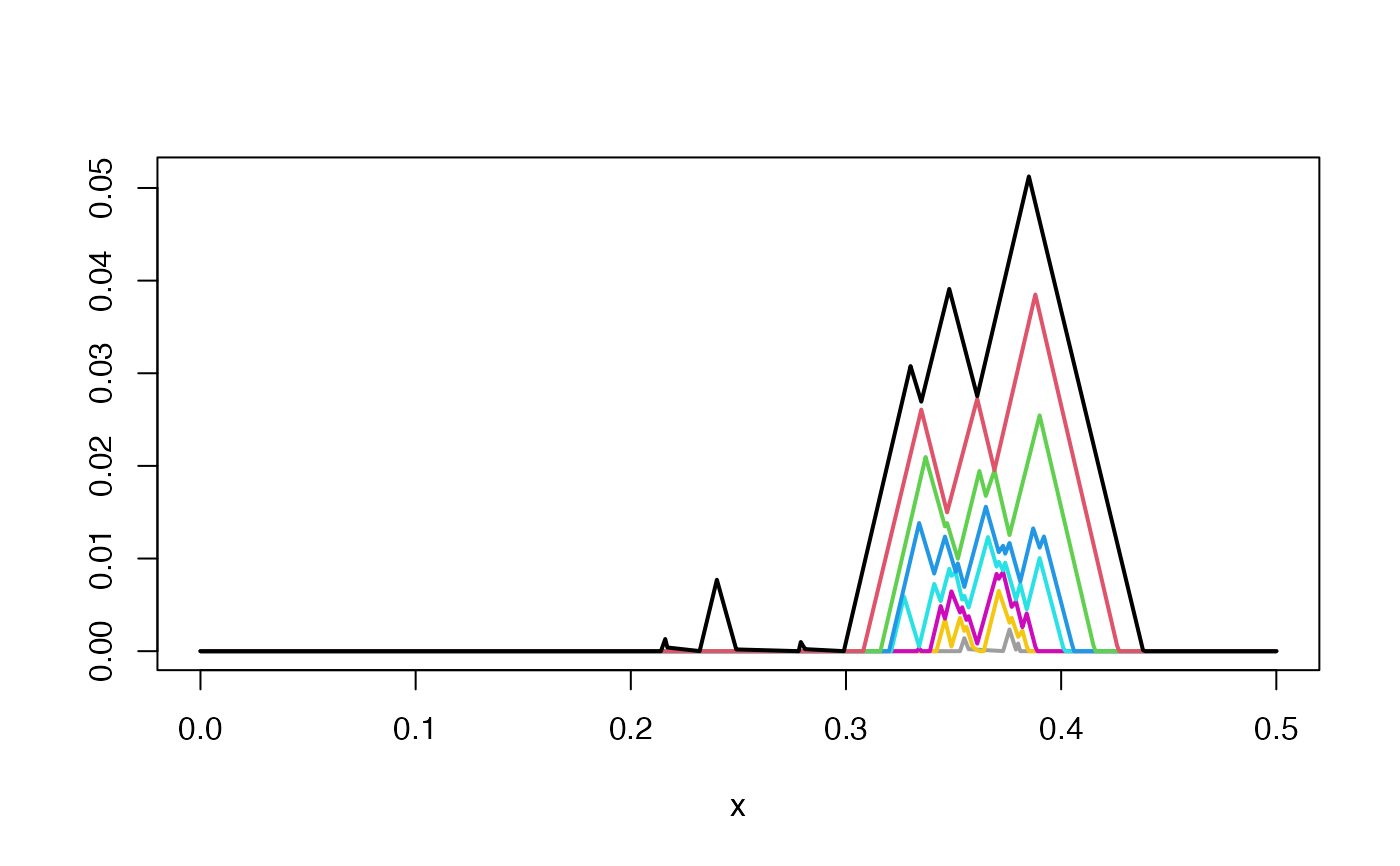
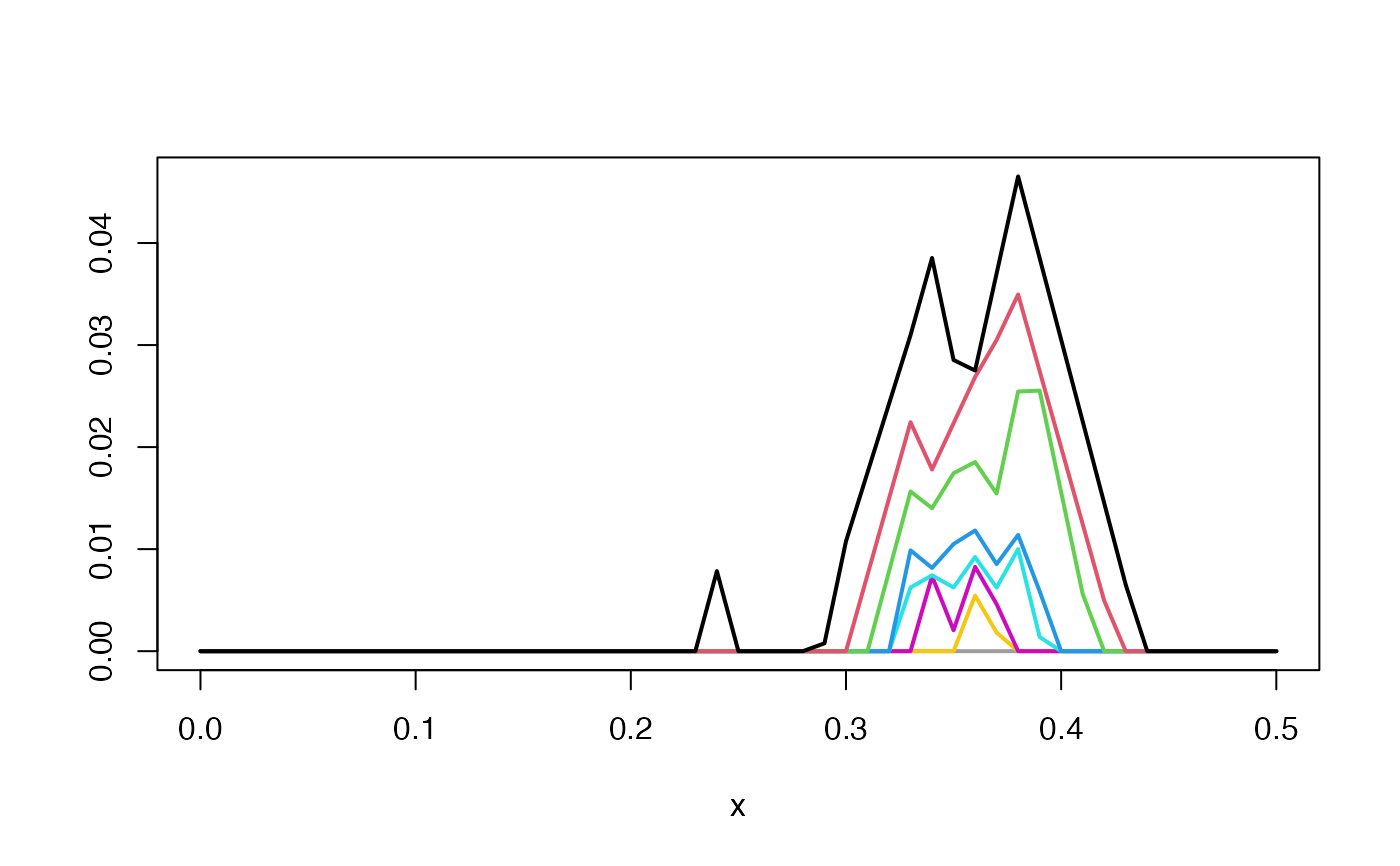 pl <- pl_delimit(pl, xmin = 0, xmax = .5, xby = .001)
pl_ <- pl_discretize(pl)
plot(pl_)
pl <- pl_delimit(pl, xmin = 0, xmax = .5, xby = .001)
pl_ <- pl_discretize(pl)
plot(pl_)
 # ensure grid when discretizing
pl_cut <- pl_discretize(pl_delimit(pl, xby = 0.1))
pl_cut$getInternal()[1, , 1]
#> [1] 0.0 0.1 0.2 0.3 0.4 0.5
pl_cut <- pl_discretize(pl_delimit(pl, xmin = 0, xmax = pi, xby = 0.1))
pl_cut$getInternal()[1, , 1]
#> [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
#> [20] 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2
# sample points
points <- tdaunif::sample_torus_tube(60L, 2.5)
# compute persistent homology
pd <- TDA::ripsDiag(points, maxdimension = 2L, maxscale = 3)
head(pd$diagram)
#> dimension Birth Death
#> [1,] 0 0 3.0000000
#> [2,] 0 0 0.5770743
#> [3,] 0 0 0.5144099
#> [4,] 0 0 0.5083332
#> [5,] 0 0 0.4868405
#> [6,] 0 0 0.4771283
# compute persistence landscape for 1-dimensional cycles
pl <- landscape(pd, degree = 1L)
print(pl)
#> Persistence landscape (discrete format) of 19 levels over (0,1.172)
# landscape dimensions
print(dim(pl$getInternal()))
#> [1] 19 119 2
# landscape values
print(head(pl$getInternal()))
#> , , 1
#>
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
#> [1,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [2,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [3,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [4,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [5,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [6,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
#> [1,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [2,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [3,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [4,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [5,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [6,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
#> [1,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [2,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [3,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [4,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [5,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [6,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49] [,50]
#> [1,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [2,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [3,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [4,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [5,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [6,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60] [,61] [,62]
#> [1,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [2,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [3,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [4,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [5,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [6,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [,63] [,64] [,65] [,66] [,67] [,68] [,69] [,70] [,71] [,72] [,73] [,74]
#> [1,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [2,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [3,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [4,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [5,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [6,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [,75] [,76] [,77] [,78] [,79] [,80] [,81] [,82] [,83] [,84] [,85] [,86]
#> [1,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [2,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [3,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [4,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [5,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [6,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [,87] [,88] [,89] [,90] [,91] [,92] [,93] [,94] [,95] [,96] [,97] [,98]
#> [1,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [2,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [3,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [4,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [5,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [6,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [,99] [,100] [,101] [,102] [,103] [,104] [,105] [,106] [,107] [,108]
#> [1,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [2,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [3,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [4,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [5,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [6,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [,109] [,110] [,111] [,112] [,113] [,114] [,115] [,116] [,117] [,118]
#> [1,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [2,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [3,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [4,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [5,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [6,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [,119]
#> [1,] 1.18
#> [2,] 1.18
#> [3,] 1.18
#> [4,] 1.18
#> [5,] 1.18
#> [6,] 1.18
#>
#> , , 2
#>
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
#> [1,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
#> [1,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
#> [1,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
#> [1,] 0 0 0 0 0 0 0 0 0 0.00878792
#> [2,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [3,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [4,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [5,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [6,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [,49] [,50] [,51] [,52] [,53] [,54]
#> [1,] 0.01878792 0.02878792 0.038787920 0.04878792 0.0587879203 0.068787920
#> [2,] 0.00000000 0.00000000 0.007192751 0.01719275 0.0271927512 0.037192751
#> [3,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0009538375 0.010953838
#> [4,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0000000000 0.009453830
#> [5,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0000000000 0.008439334
#> [6,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0000000000 0.001519955
#> [,55] [,56] [,57] [,58] [,59] [,60]
#> [1,] 0.07878792 0.08878792 0.09878792 0.108787920 0.118787920 0.128787920
#> [2,] 0.04719275 0.05719275 0.06719275 0.077192751 0.087192751 0.088336080
#> [3,] 0.02095384 0.02945383 0.03945383 0.049453830 0.059453830 0.069453830
#> [4,] 0.01945383 0.02843933 0.03843933 0.048439334 0.058439334 0.068439334
#> [5,] 0.01843933 0.02627290 0.01627290 0.021674336 0.031674336 0.041674336
#> [6,] 0.01151996 0.02151996 0.01535557 0.006272901 0.006534473 0.005663143
#> [,61] [,62] [,63] [,64] [,65] [,66]
#> [1,] 0.131542859 0.12154286 0.11154286 0.10945383 0.11945383 0.12945383
#> [2,] 0.079453830 0.08945383 0.09945383 0.10843933 0.11843933 0.12843933
#> [3,] 0.078439334 0.08843933 0.09843933 0.10154286 0.09167434 0.09355626
#> [4,] 0.078336080 0.06833608 0.07167434 0.08167434 0.09154286 0.08154286
#> [5,] 0.051674336 0.06167434 0.05833608 0.04833608 0.04622350 0.05622350
#> [6,] 0.008853565 0.01622350 0.02622350 0.03622350 0.03874563 0.03230240
#> [,67] [,68] [,69] [,70] [,71] [,72]
#> [1,] 0.13843933 0.14843933 0.15843933 0.16843933 0.17843933 0.18843933
#> [2,] 0.12876960 0.11876960 0.10876960 0.09876960 0.08876960 0.07876960
#> [3,] 0.08355626 0.07622350 0.08622350 0.07688136 0.06688136 0.05688136
#> [4,] 0.07154286 0.07355626 0.06355626 0.05673675 0.06264940 0.05264940
#> [5,] 0.06622350 0.06154286 0.05154286 0.05355626 0.04355626 0.03355626
#> [6,] 0.02673675 0.03673675 0.04673675 0.04154286 0.03154286 0.02154286
#> [,73] [,74] [,75] [,76] [,77] [,78]
#> [1,] 0.19843933 0.20843933 0.21843933 0.22843933 0.238439334 0.248439334
#> [2,] 0.06876960 0.05876960 0.04876960 0.03876960 0.046851392 0.038590577
#> [3,] 0.04688136 0.03688136 0.02688136 0.03685139 0.028769597 0.018769597
#> [4,] 0.04264940 0.03264940 0.02685139 0.01688136 0.006881359 0.001951833
#> [5,] 0.02355626 0.01685139 0.02264940 0.01264940 0.002649396 0.000000000
#> [6,] 0.01154286 0.01355626 0.00708850 0.00000000 0.000000000 0.000000000
#> [,79] [,80] [,81] [,82] [,83] [,84]
#> [1,] 0.258439334 0.26843933 0.278439334 0.288439334 0.2984393 0.3084393
#> [2,] 0.028590577 0.02154742 0.011547419 0.001547419 0.0000000 0.0000000
#> [3,] 0.011951833 0.01859058 0.008590577 0.000000000 0.0000000 0.0000000
#> [4,] 0.008769597 0.00000000 0.000000000 0.000000000 0.0000000 0.0000000
#> [5,] 0.000000000 0.00000000 0.000000000 0.000000000 0.0000000 0.0000000
#> [6,] 0.000000000 0.00000000 0.000000000 0.000000000 0.0000000 0.0000000
#> [,85] [,86] [,87] [,88] [,89] [,90] [,91]
#> [1,] 0.3184393 0.3216474 0.3116474 0.3016474 0.2916474 0.2816474 0.2716474
#> [2,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [,92] [,93] [,94] [,95] [,96] [,97] [,98]
#> [1,] 0.2616474 0.2516474 0.2416474 0.2316474 0.2216474 0.2116474 0.2016474
#> [2,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [,99] [,100] [,101] [,102] [,103] [,104] [,105]
#> [1,] 0.1916474 0.1816474 0.1716474 0.1616474 0.1516474 0.1416474 0.1316474
#> [2,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [,106] [,107] [,108] [,109] [,110] [,111] [,112]
#> [1,] 0.1216474 0.1116474 0.1016474 0.09164742 0.08164742 0.07164742 0.06164742
#> [2,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [,113] [,114] [,115] [,116] [,117] [,118] [,119]
#> [1,] 0.05164742 0.04164742 0.03164742 0.02164742 0.01164742 0.001647417 0
#> [2,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [3,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [4,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [5,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [6,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#>
# plot landscape
plot(pl)
# ensure grid when discretizing
pl_cut <- pl_discretize(pl_delimit(pl, xby = 0.1))
pl_cut$getInternal()[1, , 1]
#> [1] 0.0 0.1 0.2 0.3 0.4 0.5
pl_cut <- pl_discretize(pl_delimit(pl, xmin = 0, xmax = pi, xby = 0.1))
pl_cut$getInternal()[1, , 1]
#> [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8
#> [20] 1.9 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3.0 3.1 3.2
# sample points
points <- tdaunif::sample_torus_tube(60L, 2.5)
# compute persistent homology
pd <- TDA::ripsDiag(points, maxdimension = 2L, maxscale = 3)
head(pd$diagram)
#> dimension Birth Death
#> [1,] 0 0 3.0000000
#> [2,] 0 0 0.5770743
#> [3,] 0 0 0.5144099
#> [4,] 0 0 0.5083332
#> [5,] 0 0 0.4868405
#> [6,] 0 0 0.4771283
# compute persistence landscape for 1-dimensional cycles
pl <- landscape(pd, degree = 1L)
print(pl)
#> Persistence landscape (discrete format) of 19 levels over (0,1.172)
# landscape dimensions
print(dim(pl$getInternal()))
#> [1] 19 119 2
# landscape values
print(head(pl$getInternal()))
#> , , 1
#>
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
#> [1,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [2,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [3,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [4,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [5,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [6,] 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13
#> [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
#> [1,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [2,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [3,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [4,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [5,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [6,] 0.14 0.15 0.16 0.17 0.18 0.19 0.2 0.21 0.22 0.23 0.24 0.25
#> [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
#> [1,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [2,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [3,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [4,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [5,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [6,] 0.26 0.27 0.28 0.29 0.3 0.31 0.32 0.33 0.34 0.35 0.36 0.37
#> [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48] [,49] [,50]
#> [1,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [2,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [3,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [4,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [5,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [6,] 0.38 0.39 0.4 0.41 0.42 0.43 0.44 0.45 0.46 0.47 0.48 0.49
#> [,51] [,52] [,53] [,54] [,55] [,56] [,57] [,58] [,59] [,60] [,61] [,62]
#> [1,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [2,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [3,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [4,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [5,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [6,] 0.5 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59 0.6 0.61
#> [,63] [,64] [,65] [,66] [,67] [,68] [,69] [,70] [,71] [,72] [,73] [,74]
#> [1,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [2,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [3,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [4,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [5,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [6,] 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.7 0.71 0.72 0.73
#> [,75] [,76] [,77] [,78] [,79] [,80] [,81] [,82] [,83] [,84] [,85] [,86]
#> [1,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [2,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [3,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [4,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [5,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [6,] 0.74 0.75 0.76 0.77 0.78 0.79 0.8 0.81 0.82 0.83 0.84 0.85
#> [,87] [,88] [,89] [,90] [,91] [,92] [,93] [,94] [,95] [,96] [,97] [,98]
#> [1,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [2,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [3,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [4,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [5,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [6,] 0.86 0.87 0.88 0.89 0.9 0.91 0.92 0.93 0.94 0.95 0.96 0.97
#> [,99] [,100] [,101] [,102] [,103] [,104] [,105] [,106] [,107] [,108]
#> [1,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [2,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [3,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [4,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [5,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [6,] 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07
#> [,109] [,110] [,111] [,112] [,113] [,114] [,115] [,116] [,117] [,118]
#> [1,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [2,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [3,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [4,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [5,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [6,] 1.08 1.09 1.1 1.11 1.12 1.13 1.14 1.15 1.16 1.17
#> [,119]
#> [1,] 1.18
#> [2,] 1.18
#> [3,] 1.18
#> [4,] 1.18
#> [5,] 1.18
#> [6,] 1.18
#>
#> , , 2
#>
#> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
#> [1,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#> [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24] [,25] [,26]
#> [1,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [,27] [,28] [,29] [,30] [,31] [,32] [,33] [,34] [,35] [,36] [,37] [,38]
#> [1,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [2,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [3,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [4,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [5,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [6,] 0 0 0 0 0 0 0 0 0 0 0 0
#> [,39] [,40] [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
#> [1,] 0 0 0 0 0 0 0 0 0 0.00878792
#> [2,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [3,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [4,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [5,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [6,] 0 0 0 0 0 0 0 0 0 0.00000000
#> [,49] [,50] [,51] [,52] [,53] [,54]
#> [1,] 0.01878792 0.02878792 0.038787920 0.04878792 0.0587879203 0.068787920
#> [2,] 0.00000000 0.00000000 0.007192751 0.01719275 0.0271927512 0.037192751
#> [3,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0009538375 0.010953838
#> [4,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0000000000 0.009453830
#> [5,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0000000000 0.008439334
#> [6,] 0.00000000 0.00000000 0.000000000 0.00000000 0.0000000000 0.001519955
#> [,55] [,56] [,57] [,58] [,59] [,60]
#> [1,] 0.07878792 0.08878792 0.09878792 0.108787920 0.118787920 0.128787920
#> [2,] 0.04719275 0.05719275 0.06719275 0.077192751 0.087192751 0.088336080
#> [3,] 0.02095384 0.02945383 0.03945383 0.049453830 0.059453830 0.069453830
#> [4,] 0.01945383 0.02843933 0.03843933 0.048439334 0.058439334 0.068439334
#> [5,] 0.01843933 0.02627290 0.01627290 0.021674336 0.031674336 0.041674336
#> [6,] 0.01151996 0.02151996 0.01535557 0.006272901 0.006534473 0.005663143
#> [,61] [,62] [,63] [,64] [,65] [,66]
#> [1,] 0.131542859 0.12154286 0.11154286 0.10945383 0.11945383 0.12945383
#> [2,] 0.079453830 0.08945383 0.09945383 0.10843933 0.11843933 0.12843933
#> [3,] 0.078439334 0.08843933 0.09843933 0.10154286 0.09167434 0.09355626
#> [4,] 0.078336080 0.06833608 0.07167434 0.08167434 0.09154286 0.08154286
#> [5,] 0.051674336 0.06167434 0.05833608 0.04833608 0.04622350 0.05622350
#> [6,] 0.008853565 0.01622350 0.02622350 0.03622350 0.03874563 0.03230240
#> [,67] [,68] [,69] [,70] [,71] [,72]
#> [1,] 0.13843933 0.14843933 0.15843933 0.16843933 0.17843933 0.18843933
#> [2,] 0.12876960 0.11876960 0.10876960 0.09876960 0.08876960 0.07876960
#> [3,] 0.08355626 0.07622350 0.08622350 0.07688136 0.06688136 0.05688136
#> [4,] 0.07154286 0.07355626 0.06355626 0.05673675 0.06264940 0.05264940
#> [5,] 0.06622350 0.06154286 0.05154286 0.05355626 0.04355626 0.03355626
#> [6,] 0.02673675 0.03673675 0.04673675 0.04154286 0.03154286 0.02154286
#> [,73] [,74] [,75] [,76] [,77] [,78]
#> [1,] 0.19843933 0.20843933 0.21843933 0.22843933 0.238439334 0.248439334
#> [2,] 0.06876960 0.05876960 0.04876960 0.03876960 0.046851392 0.038590577
#> [3,] 0.04688136 0.03688136 0.02688136 0.03685139 0.028769597 0.018769597
#> [4,] 0.04264940 0.03264940 0.02685139 0.01688136 0.006881359 0.001951833
#> [5,] 0.02355626 0.01685139 0.02264940 0.01264940 0.002649396 0.000000000
#> [6,] 0.01154286 0.01355626 0.00708850 0.00000000 0.000000000 0.000000000
#> [,79] [,80] [,81] [,82] [,83] [,84]
#> [1,] 0.258439334 0.26843933 0.278439334 0.288439334 0.2984393 0.3084393
#> [2,] 0.028590577 0.02154742 0.011547419 0.001547419 0.0000000 0.0000000
#> [3,] 0.011951833 0.01859058 0.008590577 0.000000000 0.0000000 0.0000000
#> [4,] 0.008769597 0.00000000 0.000000000 0.000000000 0.0000000 0.0000000
#> [5,] 0.000000000 0.00000000 0.000000000 0.000000000 0.0000000 0.0000000
#> [6,] 0.000000000 0.00000000 0.000000000 0.000000000 0.0000000 0.0000000
#> [,85] [,86] [,87] [,88] [,89] [,90] [,91]
#> [1,] 0.3184393 0.3216474 0.3116474 0.3016474 0.2916474 0.2816474 0.2716474
#> [2,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [,92] [,93] [,94] [,95] [,96] [,97] [,98]
#> [1,] 0.2616474 0.2516474 0.2416474 0.2316474 0.2216474 0.2116474 0.2016474
#> [2,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [,99] [,100] [,101] [,102] [,103] [,104] [,105]
#> [1,] 0.1916474 0.1816474 0.1716474 0.1616474 0.1516474 0.1416474 0.1316474
#> [2,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
#> [,106] [,107] [,108] [,109] [,110] [,111] [,112]
#> [1,] 0.1216474 0.1116474 0.1016474 0.09164742 0.08164742 0.07164742 0.06164742
#> [2,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [3,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [4,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [5,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [6,] 0.0000000 0.0000000 0.0000000 0.00000000 0.00000000 0.00000000 0.00000000
#> [,113] [,114] [,115] [,116] [,117] [,118] [,119]
#> [1,] 0.05164742 0.04164742 0.03164742 0.02164742 0.01164742 0.001647417 0
#> [2,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [3,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [4,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [5,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#> [6,] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.000000000 0
#>
# plot landscape
plot(pl)
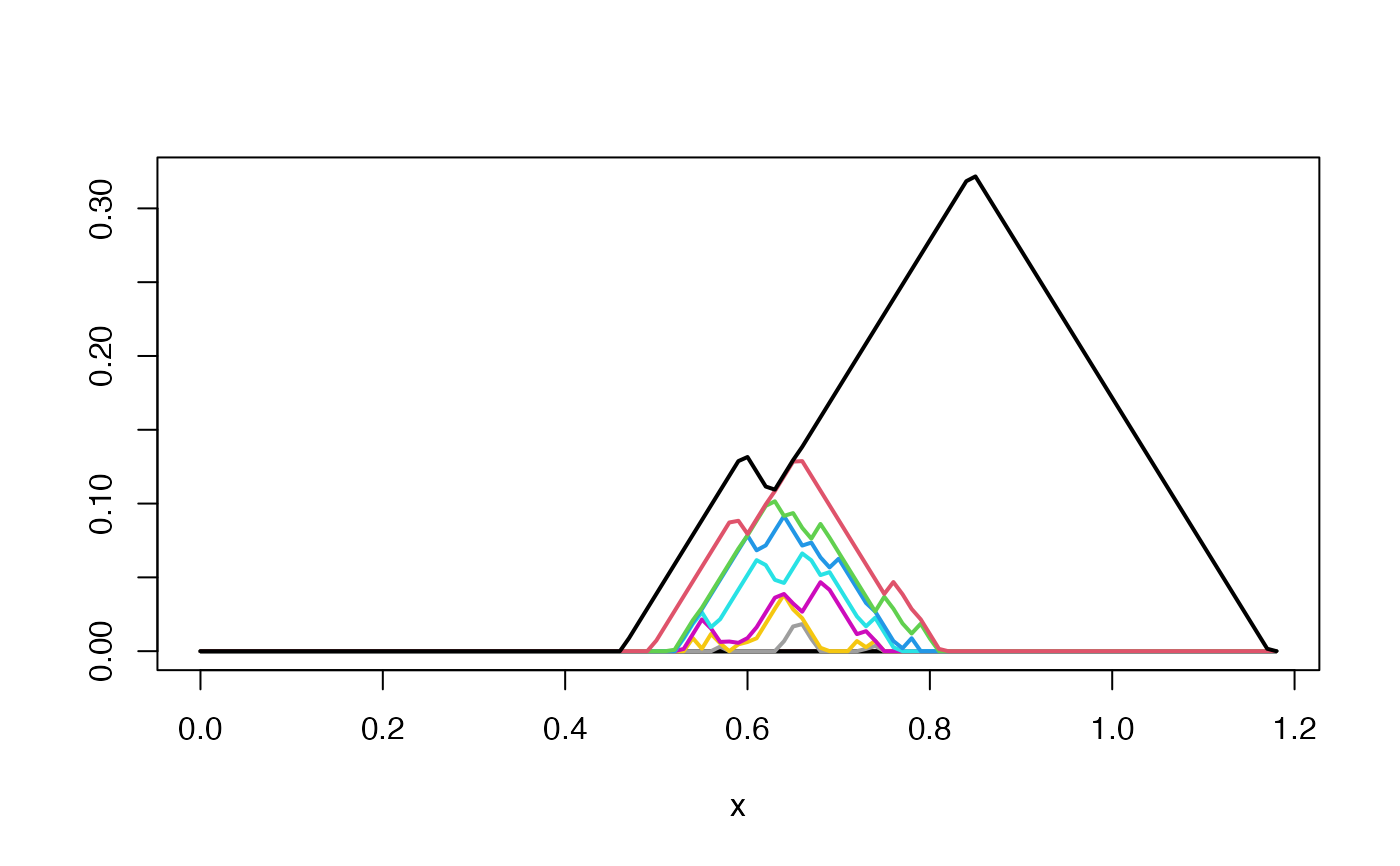 # custom parameters
pl <- landscape(pd, degree = 1L, xby = 0.1, xmax = 2)
print(pl)
#> Persistence landscape (discrete format) of 19 levels over (0,2)
plot(pl)
# custom parameters
pl <- landscape(pd, degree = 1L, xby = 0.1, xmax = 2)
print(pl)
#> Persistence landscape (discrete format) of 19 levels over (0,2)
plot(pl)